Deep Learning: Which Loss and Activation Functions should I use?
The purpose of this post is to provide guidance on which combination of final-layer activation function and loss function should be used in a neural network depending on the business goal.
This post assumes that the reader has knowledge of activation functions. An overview on these can be seen in the prior post: Deep Learning: Overview of Neurons and Activation Functions
What are you trying to solve?
Like all machine learning problems, the business goal determines how you should evaluate it’s success.
Are you trying to predict a numerical value?
Examples: Predicting the appropriate price of a product, or predicting the number of sales each day
If so, see the section Regression: Predicting a numerical value
Are you trying to predict a categorical outcome?
Examples: Predicting objects seen in an image, or predicting the topic of a conversation
If so, you next need to think about how many classes there are and how many labels you wish to find.
If your data is binary, it is or isn’t a class (e.g. fraud, diagnosis, likely to make a purchase), see the section Categorical: Predicting a binary outcome
If you’ve multiple classes (e.g. objects in an image, topics in emails, suitable products to advertise) and they are exclusive — each item only has one label — see Categorical: Predicting a single label from multiple classes. If there are multiple labels in your data then you should look to section Categorical: Predicting multiple labels from multiple classes.
Regression: Predicting a numerical value
E.g. predicting the price of a product
The final layer of the neural network will have one neuron and the value it returns is a continuous numerical value.
To understand the accuracy of the prediction, it is compared with the true value which is also a continuous number.
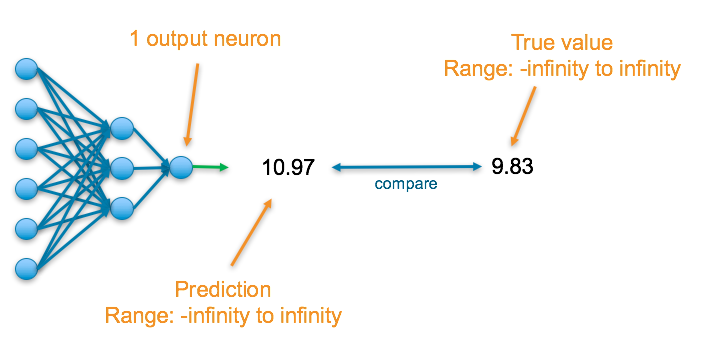
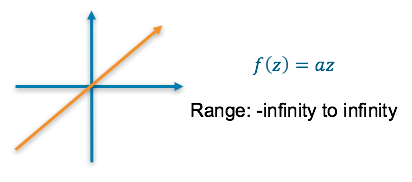
Final Activation Function
Linear — This results in a numerical value which we require
Loss Function
Mean squared error (MSE) — This finds the average squared difference between the predicted value and the true value
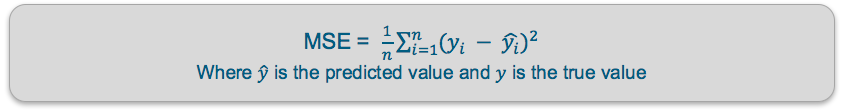
Categorical: Predicting a binary outcome
E.g. predicting a transaction is fraud or not
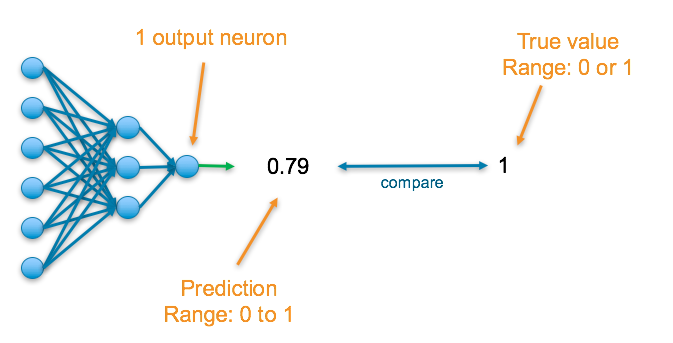
The final layer of the neural network will have one neuron and will return a value between 0 and 1, which can be inferred as a probably.
To understand the accuracy of the prediction, it is compared with the true value. If the data is that class, the true value is a 1, else it is a 0.
Final Activation Function
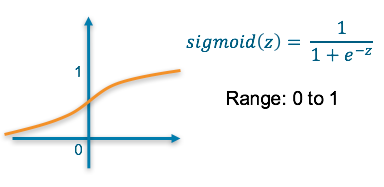
Sigmoid — This results in a value between 0 and 1 which we can infer to be how confident the model is of the example being in the class
Loss Function
Binary Cross Entropy — Cross entropy quantifies the difference between two probability distribution. Our model predicts a model distribution of {p, 1-p} as we have a binary distribution. We use binary cross-entropy to compare this with the true distribution {y, 1-y}
Categorical: Predicting a single label from multiple classes
E.g. predicting the document’s subject
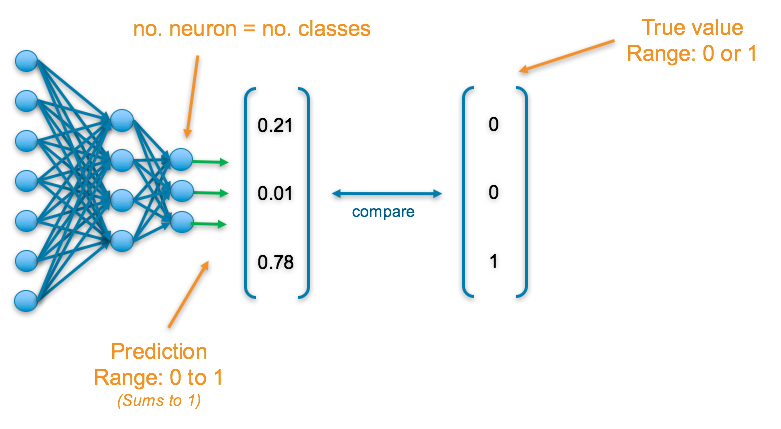
The final layer of the neural network will have one neuron for each of the classes and they will return a value between 0 and 1, which can be inferred as a probably. The output then results in a probability distribution as it sums to 1.
To understand the accuracy of the prediction, each output is compared with its corresponding true value. True values have been one-hot-encoded meaning a 1 appears in the column corresponding to the correct category, else a 0 appears
Final Activation Function
Softmax — This results in values between 0 and 1 for each of the outputs which all sum up to 1. Consequently, this can be inferred as a probability distribution
Loss Function
Cross Entropy — Cross entropy quantifies the difference between two probability distribution. Our model predicts a model distribution of {p1, p2, p3} (where p1+p2+p3 = 1). We use cross-entropy to compare this with the true distribution {y1, y2, y3}
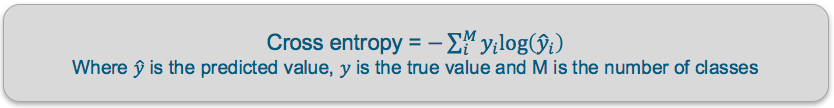
Categorical: Predicting multiple labels from multiple classes
E.g. predicting the presence of animals in an image
The final layer of the neural network will have one neuron for each of the classes and they will return a value between 0 and 1, which can be inferred as a probably.
To understand the accuracy of the prediction, each output is compared with its corresponding true value. If 1 appears in the true value column, the category it corresponds to is present in the data, else a 0 appears.
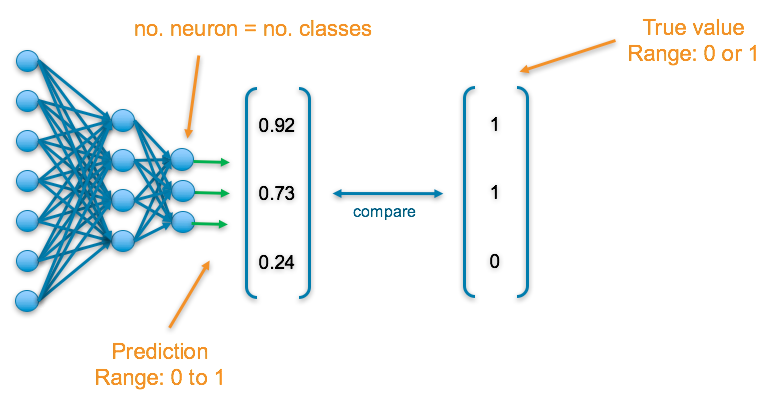
Final Activation Function
Sigmoid — This results in a value between 0 and 1 which we can infer to be how confident it is of it being in the class
Loss Function
Binary Cross Entropy — Cross entropy quantifies the difference between two probability distribution. Our model predicts a model distribution of {p, 1-p} (binary distribution) for each of the classes. We use binary cross-entropy to compare these with the true distributions {y, 1-y} for each class and sum up their results
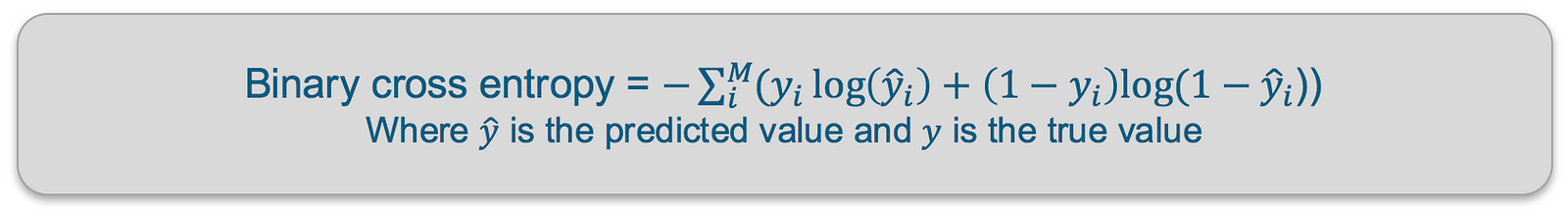
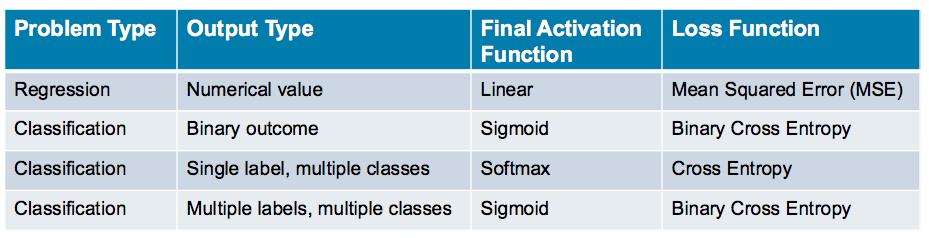
Summary Table
The following table summarizes the above information to allow you to quickly find the final layer activation function and loss function that is appropriate to your use-case
I hope this post was valuable! For further information on neural networks and final activation functions, please see the prior post:
Transforming Enterprises with
Data & AI Services & Solutions.
ThirdEye delivers Data and AI services & solutions for enterprises worldwide by
leveraging state-of-the-art Data & AI technologies.
